GLOSARIO
Punto: Es uno de los entes fundamentales, junto con la recta y el plano. Son considerados conceptos primarios, es decir, que sólo es posible describirlos en relación con otros elementos similares o parecidos. Se suelen describir apoyándose en los postulados característicos, que determinan las relaciones entre los entes geométricos fundamentales.El punto es una figura geométrica sin dimensión, tampoco tiene longitud, área, volumen, ni otro ángulo dimensional. No es un objeto físico. Describe una posición en el espacio, determinada respecto de un sistema de coordenadas preestablecidas.
Punto
Linea: Una línea funciona como una sucesión continua de puntos trazados, como por ejemplo un trazo o un guion. Las líneas suelen utilizarse en la composición artística, se denomina en cambio «raya» a trazos rectos sueltos, que no forman una figura o forma en particular.
Angulo
Linea: Una línea funciona como una sucesión continua de puntos trazados, como por ejemplo un trazo o un guion. Las líneas suelen utilizarse en la composición artística, se denomina en cambio «raya» a trazos rectos sueltos, que no forman una figura o forma en particular.
En matemáticas y geometría, línea suele denotar línea recta o curva
En geometría, la línea también puede considerarse la distancia más corta entre dos puntos puestos en un plano.
El otro concepto de la línea desde la teoría de Kandinsky es, la línea geométrica es un ente invisible. La línea es un punto en movimiento sobre el plano; al destruirse el reposo del punto este se mueve por el espacio dando origen a la línea.
La línea es el elemento más básico de todo grafismo y uno de los sumamente utilizados. Representa a la forma de expresión más sencilla y pura, que a la vez puede ser dinámica y variada. Enrique Lipszyc expresa: la línea que define un contorno es una invención de los dibujantes, ya que «en la naturaleza un objeto es distinguido de otro por su diferencia de color o de tono.» Hay varios tipos de líneas, están la línea expresiva y la línea de contorno.
Linea recta: Cuando los puntos siguen siempre la misma dirección, forman una línea recta. Imagina que pudiésemos ver cada uno de los puntos que forman una línea recta separados, entonces las veríamos así.
Una recta es una línea recta infinita: no tiene ningún límite. Como eso sería imposible de representar, dibujamos las rectas sin un punto en ninguno de sus extremos, entendiendo que eso significa que no terminan ahí sino que continúan hasta el infinito.
Semirrecta: para saber su etimología a esta palabra hay que dividirla en dos: semi y por otra parte recta. Semi significa medio o casi, esta palabra proviene del latín y es usada en palabras compuestas. Por su parte recta viene del latín rectus, que quiere decir derecho y es el participativo del verbo regere, que significa enderezar, dicho verbo se encuentra asociado con la raíz indoeuropea reg, que están presente en palabras como regla y rio.
En otras palabras donde se encuentra la raíz rectus: rectángulo, rector, rectal, rectoría, etc.
Clase: Sustantivo, femenino, singular.
Segmento de línea recta: Un segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos, llamados puntos extremos o finales.
Así, dado dos puntos A y B, se le llama segmento AB a la intersección de la semirrecta de origen A que contiene al punto B con la semirrecta de origen B que contiene al punto A. Los puntos A y B son extremos del segmento y los puntos sobre la recta a la que pertenece el segmento (la «recta sostén»), serán interiores o exteriores al segmento según pertenezcan o no a este.
Ángulo: es una magnitud física adimensional que se define como la razón entre la longitud del arco de circunferencia trazado entre dos semirrectas y su distancia al centro o vértice de las mismas que lo limitan. Esta relación nos da una idea de la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice.Su unidad natural es el radián, aunque habitualmente para evitar el uso de múltiplos de π, se utilizan equivalencias como son el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
Sistemas de medición de ángulos (Grados (decimal y sexagesimal) y Radianes). Como convertir de grados a radianes y de grados decimales a grados sexagesimales
Notación decimal:
Una cantidad en grados se puede expresar en forma decimal, separando la parte entera de la fraccionaria con la coma decimal, se divide en 60 en la forma normal de expresar cantidades decimales, lo que se busca es transformar en minuto y el segundo números decimales.
Grado sexagesimal:
Un grado sexagesimal es el ángulo central subtendido por un arco cuya longitud es igual a 1/360 de la circunferencia. Es la nonagésima (1/90) parte de un ángulo recto.
Radián:
Es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del radio. Su símbolo es rad. Hasta 1995 tuvo la categoría de unidad suplementaria en el Sistema Internacional de Unidades, junto con el estereorradián. A partir de ese año, y hasta el momento presente, ambas unidades figuran en la categoría de unidades derivadas.
Esta unidad se utiliza primordialmente en física, cálculo infinitesimal, trigonometría, goniometría, etc.
De grados a radianes:
El sistema sexagesimal es el que normalmente se emplea para medir ángulos. Para este sistema la circunferencia se divide en 360 parte que se les llaman grados, los grados en 60 partes llamadas minutos y los minutos en 60 partes llamadas segundo. Es decir, 1° =60’ y 1’=60’’.
Para el sistema cíclico o circular la unidad fundamental es el radián (rad). Un radián es la medida del ángulo central subtendido por un arco de longitud igual al radio de la circunferencia. Un radián equivale a 57.29° y ᴨ rad equivale a 180°.
Entonces, para convertir grados a radianes se utiliza la siguiente equivalencia:
180°= ᴨ rad.
Es decir, para convertir grados a radianes se multiplican los grados por una fracción que está compuesta por ᴨ rad en el numerador y180° en el denominador. Los grados se escriben en el denominador para poder eliminar las unidades de grados y así conservar sólo los radianes.
De decimal a sexagesimal:
El sistema sexagesimal es uno de los sistemas que existen para medirmagnitudes angulares. Se basa en tres órdenes de magnitud: grados (°),minutos (') y segundos ('').Como su nombre indica, es un sistema de base 60: cada 60 segundos, seañade un minuto y cada 60 minutos se añade un grado, hasta completar los360° que tiene el desarrollo completo de un círculo.Por lo tanto, si en un lugar vemos una medida como por ejemplo 43° 12'34.2'' ya sabemos que son
grados sexagesimales (sexas), ya se trate decoordenadas geográficas o de cualquier otra medida angular. Quiero decir,que
las coordenadas geográficas (lat/lon) ya están en gradossexagesimales, no hay que transformar nada!!!
Otra cosa es su expresión en grados decimales (que son grados sexagesimales expresados en notación decimal)
Entonces sí que cabe
hacer las transformaciones a las que os referíais arriba de dividir por 60 lossegundos y sumar el resultados a los minutos, dividir por 60 los minutos ysumar el resultado a los grados (por ejemplo, los 43° 12' 34.2'' seexpresarían en forma decimal como 43.2095°). Generalmente los SIGexpresan los grados sexagesimales bajo la notación decimal.Ojo! no hay que confundir los grados decimales (osea, los sexagesimalesexpresados bajo notación decimal), con los
grados centesimales
, queson
otro de los sistemas de medida de ángulos
. Una expresión degrados centesimales, es por ejemplo, 12g 45c 13cc (12 grados, 45 minutosy 13 segundos). Este tipo de grados se utilizan mucho en topografía paramedir ángulos (no tanto para expresar coordenadas geográficas) porque sonalgo más cómodos de usar que los sexas.
No son equivalentes
: una vuelta
completa de circunferencia en centesimales son 400 grados, mientras que ensexas son 360°. Cada grado centesimal por su parte tiene 100 minutoscentesimales y cada minuto 100 segundos centesimales.Para la conversión entre grados sexagesimales y centesimales se utilizageneralmente otra de las unidades que más se manejan para medirmagnitudes angulares:
los radianes
. Hay 6.283185307 radianes en unavuelta de círculo (2*PI), luego un radián equivale a 206264'8062471segundos de arco (segundos sexas; generalmente se admite 206265 entodos los cálculos), y este mismo radián equivale a 636620 segundoscentesimales.
(Grados (decimal y sexagesimal) y Radianes)de grados a radianes y de grados decimales a grados sexagesimales
Clasificación de ángulos según su medida:
Ángulos rectos : es aquel cuya medida es de 90°
Ángulo agudo : es aquel cuya medida es menor que 90°
Ángulo obtuso : es aquel cuya medida es mayor que 90° y menor que 180°
Angulo llano : mide 180 grados
Angulo Cóncavo : Dos rectas con un origen común determinan siempre dos porciones del plano y por tanto dos ángulos, α y β .
Al ángulo α se le llama ángulo convexo , mientras que el ángulo β es cóncavo.
Angulo perigonal : Es el ángulo cuyos lados coincide. Equivale a cuatro ángulos rectos y mide 360°.
Opuestos por el vertice : En geometría euclidiana dadas dos rectas r y s, del plano, que se cortan en el punto P, dos ángulos se dicen opuestos por el vértice cuando los lados de uno son semirrectas opuestas a los lados del otro ángulo.
Adyacentes : .En matemáticas se refiere a los ángulos que disponen de un lado y el vértice en común, y cuando sus otros lados resultan semirrectas opuestas, se conocen como ángulos adyacentes.
Los ángulos complementarios : Son aquellos ángulos cuyas medidas suman 90° (grados sexagesimales). Si dos ángulos complementarios son consecutivos, los lados no comunes de los dos forman un ángulo recto.
Suplementarios : Dos ángulos y son ángulos suplementarios, si suman 180° (grados sexagesimales). Un ángulo es o tienesuplementario si es menor que 180º.
Opuestos por el vertice , Adyacentes , Los ángulos complementarios , Suplementarios
Triángulo : Un triángulo, en geometría plana, es un polígono de tres segmentos que determinan tres puntos del plano no colineales. Cada punto dado pertenece a dos segmentos.1 Los puntos comunes a cada par de segmentos se denominan vértices del triángulo2 y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. Un triángulo es una figura estrictamente convexa.
Un triángulo tiene tres ángulos interiores, tres pares congruentes de ángulos exteriores,3 tres lados y tres vértices entre otros elementos.
Si está contenido en una superficie plana se denomina triángulo, o trígono, un nombre menos común para este tipo de polígonos. Si está contenido en una superficie esférica se denomina triángulo esférico. Representado, en cartografía, sobre la superficie terrestre, se llama triángulo geodésico.
Triángulo : Un triángulo, en geometría plana, es un polígono de tres segmentos que determinan tres puntos del plano no colineales. Cada punto dado pertenece a dos segmentos.1 Los puntos comunes a cada par de segmentos se denominan vértices del triángulo2 y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. Un triángulo es una figura estrictamente convexa.
Un triángulo tiene tres ángulos interiores, tres pares congruentes de ángulos exteriores,3 tres lados y tres vértices entre otros elementos.
Si está contenido en una superficie plana se denomina triángulo, o trígono, un nombre menos común para este tipo de polígonos. Si está contenido en una superficie esférica se denomina triángulo esférico. Representado, en cartografía, sobre la superficie terrestre, se llama triángulo geodésico.
Triángulo
Clasificación de los triángulos por sus lados :
1) triángulos equiláteros
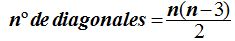
Clasificación de los triángulos por sus lados.
Clasificación de los triángulos por sus ángulos :
1) Triángulos rectángulos si tienen UN ángulo recto.
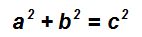
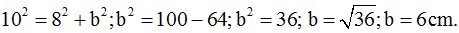
Figura geométrica plana, limitada por una poligonal cerrada que no se cortan a si mismas.
Clasificación de los triángulos por sus lados :
1) triángulos equiláteros
Las palabras equi - látero vienen del latín: igual – lado.
Son los triángulos cuyos tres lados son iguales: 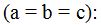
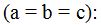
2) triángulos isósceles
La palabra isósceles está compuesta de dos palabras griegas isoque significa igual y de la palabra skeles que podemos traducir por piernas.
La palabra isósceles referido a la geometría quiere decir que dos lados (piernas) son iguales. Por lo tanto, un triángulo con dos lados iguales llamamos isósceles.
Como ves en la figura, tienes el triángulo isósceles con dos lados iguales. Si tiene 2 lados iguales tendrá también dos ángulos iguales.
3) triángulos escalenos
La palabra escaleno procede de la palabra griega skaleno que significa cojear, cojo. Nos da la idea que si el triángulo “cojea” sus lados no son iguales. Efectivamente, el triángulo escaleno tiene sus lados diferentes por lo que sus ángulos también serán diferentes.
15.67 ¿Sería correcto decir que en un triángulo equilátero cada ángulo mide 59º38’56’’?
Respuesta: Incorrecto. Cada ángulo debe medir 60º porque la suma de todos es 180º y como son iguales basta que dividas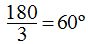
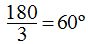
15.68 En un triángulo isósceles, cada uno de los ángulos iguales mide 30º16’ ¿Cuánto vale el ángulo desigual?
Respuesta: 119º28’
15.69 El triángulo que tienes en la figura siguiente ¿qué tipo de triángulo es, según sus lados y cuánto mide el ángulo X?
Respuestas: Escaleno y el ángulo X vale 56º06’
15.70 ¿Puede existir un triángulo cuyos ángulos miden 66º56’44’’, 43º12’33’’ y 69º50’43’’?¿Por qué?
Respuesta: Sí, porque la suma de sus ángulos es 180º
15.71 ¿Qué clase de triángulo es el que tiene por ángulos 65º43’58’’, 55º37’55’’ y 63º12’13’’?
Respuesta: No existe. La suma de sus ángulos superan 180º
15.72 En un triángulo isósceles el ángulo desigual vale 66º14’34’’ ¿Cuánto vale cada uno de los ángulos iguales?
Respuesta: 56º52’43”
15.73 ¿Cuántas diagonales tiene un triángulo? Razona la respuesta.
Respuesta: No tiene ninguna.
Explicación: Recuerda que diagonal es una recta que uno dos vértices no consecutivos de un polígono o de un poliedro (estudiaremos más adelante) . En un triángulo es imposible dibujar una diagonal que una dos vértices no consecutivos. Porque si parto de un vértice y voy al 2º no consecutivo me encuentro con un lado del triángulo.
Debes tener en cuenta de que cada vértice salen tantas diagonales como lados tiene el polígono menos 3 pero las contamos dos veces.
Del cuadrado saldrían: 4 (vértices)x(4 – 3) = 4, pero se repetirían la mitad de las diagonales, luego, el número de diagonales del cuadrado serán 2.
El pentágono tendrá: 5 (vértices)x(5 – 3) =5x2 = 10 pero repetiríamos la mitad, 5 diagonales (las tendríamos trazadas con anterioridad). Nos quedan 10 – 5 = 5 diagonales. El hexágono tendrá: 6 (vértices)x(6 – 3) =6x3 = 18 pero repetiríamos 9 diagonales (las tendríamos trazadas con anterioridad). Nos quedan 18 – 9 =9 diagonales.
El heptágono tiene: 7 (vértices)x(7 – 3) =7x4 = 28 pero repetiríamos, las mitades, 14 diagonales (las tendríamos trazadas con anterioridad). Nos quedan 28 – 14 =14 diagonales.
Para hacer el cálculo más sencillo aplicas la fórmula
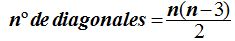
representando por n el número de lados del polígono:
15.74 Cuántas diagonales tiene un polígono de 28 lados?
Respuesta: 350 diagonales
15.75 En un triángulo, ¿puede uno de sus ángulos ser cóncavo?
Respuesta: No, porque un ángulo cóncavo vale más de 180º
Los dos lados a y b de la figura forman un ángulo cóncavo de 225º y para trazar el tercer lado del triángulo vemos que nos es imposible.
Clasificación de los triángulos por sus lados.
Clasificación de los triángulos por sus ángulos :
1) Triángulos rectángulos si tienen UN ángulo recto.
Tienes a continuación tres ejemplos de triángulos rectángulos
En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa y los lados perpendiculares que forman el ángulo recto se llaman catetos.
Teorema de Pitágoras: Al estudiar el triángulo rectángulo hemos de conocer perfectamente este teorema que nos dice:
En todo triángulo rectángulo, la suma de los cuadrado de los catetos es igual al cuadrado de la hipotenusa
Tomemos como ejemplo el de la figura en el que los catetos miden 3 y 4 cm., respectivamente y 5 cm., la hipotenusa.
Con las medidas de los catetos formamos cuadrados 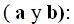
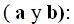
Con la longitud de la hipotenusa formamos otro cuadrado (c):
Si calculas el área del cuadrado formado por el cateto (a): lado al cuadrado obtienes como valor del área: 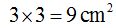
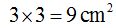
Si a continuación calculas el cuadrado formado por el cateto (b), el valor de su área vale 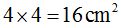
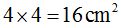
El cuadrado formado por la longitud de la hipotenusa tiene un área de 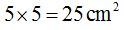
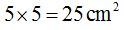
Si sumas las áreas de los cuadrados de los catetos, es decir 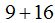 obtienes el área formada por el cuadrado de la hipotenusa,
obtienes el área formada por el cuadrado de la hipotenusa, 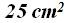
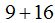 obtienes el área formada por el cuadrado de la hipotenusa,
obtienes el área formada por el cuadrado de la hipotenusa, 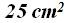
Fíjate en la figura siguiente:
La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.Siendo a y b las longitudes de los catetos los catetos, y c la longitud de la hipotenusa podemos escribir:
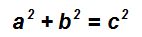
Resuelve:
(a) Calcula la longitud de la hipotenusa de un triángulo rectángulo sabiendo que los catetos miden 5 y 6 cm., respectivamente.
El resultado es de 7,81 cm. porque la suma de los cuadrados de los catetos es 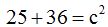 de donde
de donde 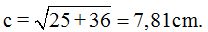
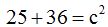 de donde
de donde 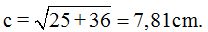
(b) Sabiendo que la hipotenusa de un triángulo rectángulo vale 10 cm., y uno de los catetos 8 cm.
¿Cuál es el valor del otro cateto?
El resultado es de 6 cm. Porque
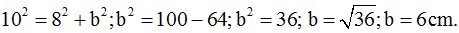
2) Triángulos acutángulos, si tienen TRES ángulos agudos(menores de 90º).
En el dibujo siguiente tienes dos triángulos acutángulos.
3) Triángulos obtusángulos, si tienen UN ángulo obtuso (más de 90º).
En la siguiente figura tienes dos triángulos obtusángulos
15.76 ¿Puede un triángulo rectángulo tener, además de su ángulo recto, dos ángulos de 56º y 45º? ¿Por qué?
Respuesta: No, porque la suma de los tres ángulos debe valer 180º y en este caso, supera ese número.
15.77 Dos triángulos isósceles tienen iguales dos lados y el ángulo comprendido entre ellos. ¿Son necesariamente iguales?
Respuesta: Sí.
15.78 ¿La suma de los ángulos no rectos de los triángulos rectángulos han de sumar un ángulo recto? ¿Por qué?
Respuesta: Sí, porque si el ángulo recto vale 90º los otros dos 2 ángulos no rectos tendrán que sumar 90º, de este modo, la suma de los ángulos del triángulo suman 180º
RELACIÓN ENTRE LOS ÁNGULOS Y LOS LADOS DE LOS TRIÁNGULOS
En los triángulos los ángulos dependen de los lados en cuanto a sus medidas, de ahí que podemos decir:
A) A mayor lado se opone mayor ángulo
Comprueba en la figura siguiente que a mayor lado, se oponemayor ángulo.
Lo mismo puede decirse a la inversa, a menor ángulo, se opone menor longitud de lado
B) En un triángulo, la longitud de un lado cualquiera es menor que la suma de las longitudes de los otros dos lados.
La suma de los dos lados menores será siempre mayor que el lado más grande.
En el primer triángulo la suma de los lados de menor longitud es mayor que la del lado de mayor longitud 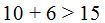
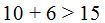
Lo mismo sucede en el segundo triángulo de la figura: 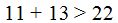
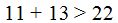
C) Si un triángulo tiene sus lados iguales también serán sus ángulos opuestos.
En la figura siguiente verás en el primer triángulo que los lados a y b al tener iguales longitudes, sus ángulos opuestos miden lo mismo.
Igualmente, en el segundo triángulo los lados x e y al tener la misma longitud, sus ángulos opuestos son iguales.
Rectas y puntos notables en el triángulo.
Rectas y puntos notables de un triángulo. Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. En los triángulos se puede denotar un grupo de rectas y puntos muy importantes. Entre las rectas notables más conocidas de un triángulo se pueden nombrar las mediatrices, las medianas, las alturas y las bisectrices; cada una de estas rectas notables determina cierto punto notable: circuncentro, baricentro, ortocentro e incentro, respectivamente.
Mediatriz: Conjunto de puntos del plano que equidistan de los puntos extremos de un segmento. Como consecuencia la mediatriz biseca perpendicularmente al segmento. En un triángulo, las tres mediatrices de sus lados concurren en un punto que equidista de los vértices del triángulo. El punto en el que se cortan las mediatrices de un triángulo, se conoce como circuncentro, o sea, el centro de la circunferencia circunscrita al triángulo de referencia. Al radio de la circunferencia circunscrita se le suele llamar circunradio y es la distancia desde el circuncentro a los vértices del triángulo. Obviando el rigor de la definición de círculo, a la circunferencia circunscrita se le llama también circuncírculo (para abreviar).Mediatriz
- En el triángulo ABC las mediatrices MAC, MBC y MAB se intersecan en el punto C que costituye el circucentro del triángulo o centro de la circunferencia circunscrita al triángulo ABC.
Mediatrices de un triángulo obtusángulo
- En el caso de los triángulos obtusángulos, el circuncentro es un punto ubicado fuera del triángulo.
Meditrices de un triángulo rectángulo
- En el caso de los triángulos rectángulos, el circuncentro es el punto medio de la hipotenusa
Mediana
Mediana:
- La mediana es el segmento de recta que se traza desde un vértice de un triángulo al punto medio de su lado opuesto.
- Las tres medianas de un triángulo concurren en un punto.
- El punto donde se cortan la medianas de un triángulo se conoce como baricentro, centroide o centro de gravedad y tiene una propiedad física muy importante: Si colocamos un eje a través de él y dejamos libre el triángulo, este no se mueve por acción de la aceleración de la gravedad, es por ello que el baricentro se llama centro de gravedad del triángulo.
- Las medianas se cortan siempre en un punto interior al triángulo.
- El baricentro divide a cada mediana en la razón 2:1. Esto es, la longitud del segmento de mediana medida desde el vértice al baricentro es el doble que desde el baricentro al punto medio del lado en cuestión.
- Cada mediana de un triángulo, lo divide en dos triángulos de igual área.
Las Alturas
- Se llama altura de un triángulo al segmento de perpendicular trazada por un vértice del triángulo y comprendido entre ese vértice y su lado opuesto.
- Las alturas de un triángulo concurren en un punto denominado ortocentro del triángulo.
- El ortocentro de un triángulo acutángulo es un punto interior del triángulo.
El ortocentro en un triangulo obtusángulo
- En el caso de un triángulo obtusángulo, el ortocentro es un punto exterior al triángulo.
- En el caso del triángulo rectángulo vemos que el ortocentro coincide con el vértice del ángulo recto.
- Los pies de las alturas de un triángulo determinan un triángulo llamado: triángulo pedal u órtico del triángulo dado.
Las bisectrices
- Bisectriz de un ángulo: Es el conjunto de puntos del plano donde está contenido el ángulo que equidista de los lados del ángulo. Como consecuencia la bisectriz de un ángulo lo divide en dos ángulos de igual amplitud.
- Todo ángulo tiene dos bisectrices, una interna y otra externa. Las bisectrices interna y externa de un ángulo son perpendiculares entre sí.
- Las bisectrices de los ángulos interiores de un triángulo concurren en un punto que equdista de los lados del triángulo, llamado incentro del triángulo o centro de la circunferencia inscrita en el triánguloy siempre es interior al triángulo. La equidistancia se llama inradio o radio de la circunferencia inscrita en el triángulo.
- Cada bisectriz interna y las bisectrices de los otros dos ángulos externos del triángulo concurren en otros tres puntos que también equidistan de los lados (o sus prolongaciones) del triángulo. Estos puntos se llaman exincentros del triángulo y las circunferencias que determinan: circunferencias exinscritas del triángulo. Algunos autores las llaman circunferencias excritas o excírculos y a sus centros excentros.
Generalidades
- Una ceviana es un segmento de recta que une un vértice de un triángulo con el lado opuesto a este. También se la conoce como transversal angular.La mediana, la altura y la bisectriz son cevianas. El nombre de ceviana fue introducido por M.A. Poulain, que lo introdujo en honor de Giovanni Ceva, quien en 1678 había formulado el teorema que lleva su nombre: Teorema de Ceva. Este teorema da la condición necesaria y suficiente para que tres cevianas se corten en un punto.
- En el triángulo equilátero coinciden todas las rectas y puntos notables tratados, es decir, las medianas, las alturas, las bisectrices y las mediatrices, así como el baricentro, el ortocentro, el incentro y el circuncenro.
- En el triángulo isósceles la altura relativa a la base, es mediana, bisectriz y mediatriz.
- El ortocentro de un triángulo coincide con el incentro de su triángulo pedal.
- Se conoce como circunferencia de los nueve puntos a una circunferencia que se puede construir sobre cualquier triángulo dado. Su nombre deriva del hecho que la circunferencia pasa por nueve puntos notables, seis de ellos sobre el mismo triángulo (excepto que el triángulo sea obtusángulo). Estos nueve puntos son: el punto medio de cada lado del triángulo, los pies de las alturas, y los puntos medios de los segmentos determinados por el ortocentro y los vértices del triángulo. A la circunferencia de los nueve puntos se le conoce también entre otros como circunferencia de Feuerbach, circunferencia de Euler, etc.
- Existen otras rectas y puntos notables del triángulo, a saber:
- La recta de Simson, las simedianas y puntos simedianos,, punto, ángulo y circunferencia de Brocard, la recta de Gauss, el punto de Miquel, la circunferencia de Lemoine, etc.
- Son teoremas importantes relacionados con las rectas y puntos notables del triaángulo, colinealidad de puntos o concurrencia de rectas, los teoremas Carnot, de Ceva, de Menelao, de Feuerbach, de Desargues, de Stewart, de Steiner, de Spieker, etc.
POLÍGONOS REGULARES E IRREGULARES
LÍNEAS POLIGONALES
Una linea poligonal es un conjunto de segmentos concatenados, (cada uno empieza donde acaba el anterior), y pueden ser: abiertas o cerradas.
La superficie contenida por una línea poligonal cerrada se llama polígono.
Polígono
Clasificación de los Polígonos
Los polígonos se clasifican básicamente en: polígonos regulares y polígonos irregulares.
Polígono Regular
Polígono en el cual todos sus lados son de igual longitud, y todos sus vértices están circunscritos en una circunferencia. Se clasifican en:
- Triángulo equilátero: polígono regular de 3 lados,
- Cuadrado: polígono regular de 4 lados,
- Pentágono regular: polígono regular de 5,
- Hexágono regular: polígono regular de 6 lados,
- Heptágono regular: polígono regular de 7 lados,
- Octágono regular: polígono regular de 8 lados,... y así sucesivamente.
POLÍGONO REGULAR
Polígono Irregular
Polígono en el cual sus lados no son de igual longitud y/o sus vértices no están contenidos en una circunferencia. De acuerdo al número de sus lados, se denominan:
- - Triángulo: polígono de 3 lados,
- - Cuadrilátero: polígono de 4 lados,
- - Pentágono: polígono de 5 lados,
- - Hexágono: polígono de 6 lados,
- - Heptágono: polígono de 7 lados,
- - Octágono: polígono de 8 lados,... y así sucesivamente.
POLÍGONO IRREGULAR
Propiedades de los polígonos:
a.Suma de los ángulos interiores
b.Número de triángulos que se forman en el interior
Suma de los ángulos interiores de un polígono
Número de triángulos que se forman en el interior
Número de triángulos que se forman en el interior
Perímetros y áreas de los polígonos
| Nombre | Dibujo | Perímetro | Área |
| Triángulo |
|
P = Suma de los lados
P = b + c + d
|
|
| Cuadrado |
| P = 4 · a | A = a2 |
| Rectángulo |
| P = 2(b + a) | A = b · a |
| Rombo |
| P = 4 · a |
|
| Romboide |
| P = 2(b + c) | A = b · a |
| Trapecio |
| P = B + c + b + d |
|
| Trapezoide |
| P = a + b + c + d |
A = Suma de las áreas de los dos triángulos
|
| Polígono regular |
|
|
|
Perímetros y áreas de los polígonos
Fórmula de Herón
En geometría plana elemental la fórmula de Herón, cuya invención se atribuye al matemático griego Herón de Alejandría,1 da el área de un triángulo conociendo las longitudes de sus tres lados a, b y c:
donde s es el semiperímetro del triángulo:
- .
Cualquier polígono simple puede ser separado en triángulos que a lo más tienen un lado común o un vértice común, mediante diagonales que parten de un único vértice apropiado. Esta subdivisión y la aplicación de la norma herodiana para el área triangular, facilita el cálculo del área de la región plana encerrada por el polígono simple, con solo medir longitudes, allí radica su importancia.
La fórmula también puede expresarse de estas otras formas:
La fórmula de Herón se distingue de otras fórmulas para hallar el área de un triángulo, como la de la mitad de la base por la altura o la de la mitad del módulo de un producto cruz de dos lados, por no requerir ninguna elección arbitraria de un lado como base o un vértice como origen.
Circunferencia Rectas y segmentos
Transcripción de Rectas, segmentos y ángulos de una circunferencia
Ángulos en una circunferencia.
1 Ángulo central
El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.
La medida de un arco es la de su ángulo central correspondiente.
2 Ángulo inscrito
El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.
Mide la mitad del arco que abarca.
Mide la mitad del arco que abarca.
3 Ángulo semi-inscrito
El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.
Mide la mitad del arco que abarca.
Mide la mitad del arco que abarca.
4 Ángulo interior
Su vértice es interior a la circunferencia y sus lados secantes a ella.
Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.
Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.
5 Ángulo exterior
Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:
Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:


















































































No hay comentarios:
Publicar un comentario